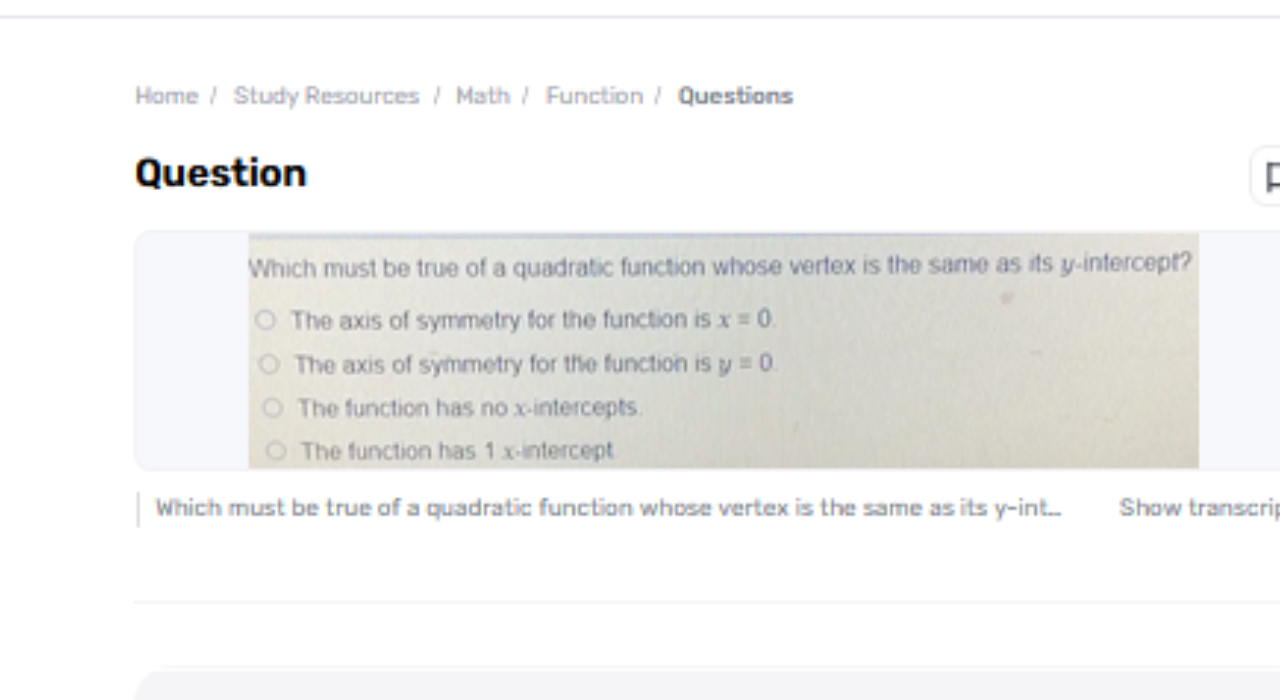
Quadratic capacities are a principal perspective of variable-based math, characterized by their allegorical charts, which can open upwards or downwards depending on the coefficient of the quadratic term. Understanding the properties of these capacities is vital for understanding different scientific issues, which must be true of a quadratic function whose vertex is the same as its y-intercept? finding roots, deciding the vertex, and analyzing the function's behavior.

In this setting, we investigate a particular condition: when the vertex of a quadratic work is the same as its y-intercept. This situation forces specific limitations on the function's shape and properties, such as rearranging to a particular condition, driving curious experiences about its structure and behavior, and uncovering the symmetrical nature of the work.

Understanding Quadratic Capacities

A quadratic work is by and large communicated within the shape f(x)=ax2+bx+cf(x) = ax^2 + bx + cf(x)=ax2+bx+c, where aaa, bbb, and ccc are constants, and a 0a new 0a =0. The chart of a quadratic work could be a parabola, The vertex of the parabola speaks to the function's most extreme or last point, and its arranges are given by (b2a,f(b2a)) left (-frac{b}{2a}, left (-frac{b} {2a}right) right)(2ab,f(2ab)). The y-intercept, on the other hand, is the point where the chart converges the y-axis, spoken to by (0,c)(0, c)(0,c).

Vertex and Y-Intercept Coincidence

For a quadratic work whose vertex is the same as its y-intercept, the vertex facilitates (b2a,f(b2a) left ( -frac{b}{2a}, left (-frac{b} {2a}right) right)(2ab,f(2ab)) must coincide with the y-intercept facilitates (0,c)(0, c)(0,c). This condition streamlines the examination because it suggests that b2a=0-frac{b}{2a} = 02ab=0. Thus, I must be zero since a 0a new 0ai =0. In this way, the quadratic work rearranges to f(x)=ax2+cf(x) = ax^2 + cf(x)=ax2+c, with no straight term shown.

Suggestions of b=0b = 0b=0

With b=0b = 0b=0, the quadratic work takes the shape f(x)=ax2+cf(x) = ax^2 + cf(x)=ax2+c. The vertex of this work is found at x=0x = 0x=0, as inferred from b2a-frac{b}{2a}2ab. Assessing the work at x=0x = 0x=0 gives f(0)=cf(0) = cf(0)=c, which matches the y-intercept. Hence, the vertex arranges are (0,c)(0, c)(0,c), affirming that the vertex and y-intercept coincide. This also implies that the parabola's symmetry hub is the y-axis itself.

The Gauth Strategy: An Organized Approach to Doing Homework

Step 1: Arrange and Organize

The Gauth Strategy includes arranging and organizing homework assignments by posting them, prioritizing them based on due dates, trouble level, and assessed time, and gathering vital materials like course readings, notes, and composing devices for each assignment.

Step 2: Center and Execute

To viably total assignments, apportion particular timepieces based on prioritization, minimize diversions, and effectively lock in with the fabric. Make a considered environment free from notices and energize calm spaces. Locks in with the fabric extends understanding and maintenance.

Step 3: Survey and Reflect

The Gauth Strategy includes investigating and reflecting on completed assignments, guaranteeing precision and completeness. It includes checking for blunders, taking after enlightening, and guaranteeing understanding. Reflecting on learning and distinguishing zones for clarification is additionally pivotal. Arranging ahead for up-and-coming assignments and altering procedures appropriately is fundamental.

Conclusion

In conclusion, a quadratic work whose vertex coincides with its y-intercept is characterized by the nonappearance of a straight term, disentangling to the shape f(x)=ax2+cf(x) = ax^2 + cf(x)=ax2+c. This results in a symmetrical parabola centered on the y-axis, with the vertex and y-intercept both found at (0,c)(0, c)(0,c). Understanding this special situation improves our comprehension of quadratic functions and their graphical representations, giving profitable bits of knowledge for both hypothetical and down-to-earth applications.